icql-blog
数据结构_树
一、定义
树是n个结点的有限集,每个结点只能有唯一的一个父结点
二、基本特性
1)概念
>(1)结点的度:结点的子项个数
>(2)树的度:结点度中的最大值
>(3)叶子结点
>(4)父结点
>(5)孩子
>(6)树的深度:树的最大层次
>(7)森林:m个互不相交的树的集合
2)特点
根结点:无父节点,唯一
叶子结点:无孩子
中间结点:一个双亲,多个孩子
三、二叉树
定义:每个结点最多有两棵子树,所以二叉树中不存在度大于2的结点;左右子树是有顺序的,即使只有一棵子树
1)性质
>(1)第i层上最多有 2^(i-1)个结点
>(2)深度为k的二叉树最多有(2^k - 1)个结点
>(3)终端结点数为n0,度数为2的结点数n2,则 n0 = n2 + 1
>(4)具有n个节点的完全二叉树深度为 log2 n +1
>(5)具有n个节点的完全二叉树深度为 log2 n +1,1 <= i <= n
>i=1,结点i是二叉树的根,无双亲
>i>1,其双亲是结点 i/2
>i>n/2,则结点i无左孩子,否则左孩子是结点 2i
>2i+1>n,则结点i无右孩子,否则其右孩子是结点 2i+1
2)存储结构
(1)顺序存储:
从根开始,按照每层从左到右依次存储,普通的二叉树若结点不是2个孩子,则以null代替,但这样比较浪费空间,所以一般只有完全二叉树使用顺序存储(数组)
(2)二叉链表:
class Node{
E e;
Node left;
Node right;
}
3)遍历
>1)前序遍历:根结点-左结点-右节点
>2)中序遍历:左结点-根结点-右节点
>3)后序遍历:左结点-右节点-根结点
>4)层序遍历:从根节点开始,每层从左到右依次遍历
>
>前、中、后遍历:都是深度优先遍历
>层序遍历:是广度优先遍历
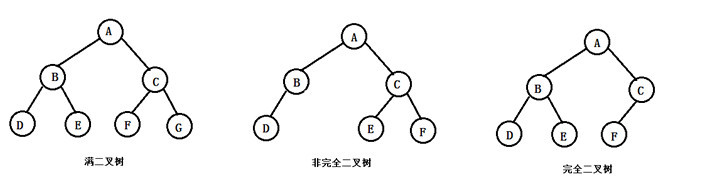
4)特殊二叉树
(1)满二叉树:
除了叶子之外所有子树都有左右孩子,且叶子均在同一层次上,是一个三角形
(2)完全二叉树:
一棵二叉树,除了最后一层之外都是完全填充的,并且最后一层的叶子结点要么都有要么只有左边
四、堆
常用的是二叉堆,是一个完全二叉树
(1)最大堆:父结点的值总是大于孩子结点的值
(2)最小堆:父结点的值总是小于孩子结点的值
1)存储
一般用数组表示,完全二叉树
性质: (1)父结点索引 = 当前结点索引/2 (2)左孩子结点索引 = 当前结点索引2 (3)右孩子结点索引 = 当前结点索引2+1
2)常用操作
package work.icql.java.datastructure.tree;
import java.util.ArrayList;
import java.util.List;
public class MaxHeap {
private List<Integer> data;
public MaxHeap() {
data = new ArrayList<>();
}
//堆化,将数组堆化,O(n),一个一个add,O(nlogn)
public MaxHeap(int[] arr) {
data = new ArrayList<>();
for (int i = parent(arr.length - 1); i >= 0; i--) {
siftDown(i);
}
}
//向堆中添加元素
//添加到数组尾部,上浮堆尾
public void add(int e) {
data.add(e);
siftUp(data.size() - 1);
}
private void siftUp(int k) {
int parent = parent(k);
while (k > 0 && data.get(parent) < data.get(k)) {
swap(k, parent);
k = parent;
}
}
//看堆中的最大元素
public int findMax() {
if (data.size() == 0) {
throw new IllegalArgumentException();
}
return data.get(0);
}
//取出堆中最大元素
//交换堆顶和尾部,删除堆尾,下沉堆顶
public int removeMax() {
int ret = findMax();
swap(0, data.size() - 1);
data.remove(data.size() - 1);
siftDown(0);
return ret;
}
private void siftDown(int k) {
while (leftChild(k) < data.size()) {
//在此轮循环中,data[k]和data[j]交换位置
int j = leftChild(k);
if (j + 1 < data.size() &&
data.get(j + 1) > data.get(j)) {
j++;
}
//data[j] 是 leftChild 和 rightChild 中的最大值
if (data.get(k) >= data.get(j)) {
break;
}
swap(k, j);
k = j;
}
}
private void swap(int a, int b) {
int aVal = data.get(a);
int bVal = data.get(b);
data.set(a, bVal);
data.set(b, aVal);
}
private int parent(int index) {
if (index == 0) {
throw new IllegalArgumentException();
}
return (index - 1) / 2;
}
private int leftChild(int index) {
return index * 2 + 1;
}
private int rightChild(int index) {
return index * 2 + 2;
}
}
3)堆的应用
(1)top n
构造一个最小堆,遍历一边所有数据,每次和堆顶比较 (1)若比堆顶大,则删除堆顶,当前元素入堆 (2)若比堆顶小,则不做操作
(2)堆排序
https://www.cnblogs.com/chengxiao/p/6129630.html
O(nlogn),不稳定排序 所有数据在一个数组里,堆化得到最大堆,将堆顶和数组末尾交换,除了数组末尾剩下的用堆顶下沉,得到最大堆,再交换,递归得到
五、二分搜索树
性质: (1)二叉树 (2)每个结点的值大于左子树所有结点的值 (3)每个结点的值小于右子树所有结点的值
二分搜索树可以作为2个条件的分类树 左子树放第一个条件 右子树放第二个条件
package work.icql.java.datastructure.tree;
import java.util.LinkedList;
import java.util.Queue;
import java.util.Stack;
public class BinarySearchTree {
private static class Node {
private int e;
private Node left;
private Node right;
public Node(int e) {
this.e = e;
}
}
private Node root;
private int size;
//region 增
public void add(int e) {
root = add(root, e);
}
/**
* 返回传入的结点
*/
private Node add(Node node, int e) {
if (node == null) {
size++;
return new Node(e);
}
int diff = e - node.e;
if (diff == 0) {
return node;
}
if (diff < 0) {
node.left = add(node.left, e);
} else {
node.right = add(node.right, e);
}
return node;
}
//endregion
//region 查
public boolean contains(int e) {
return contains(root, e);
}
private boolean contains(Node node, int e) {
if (node == null) {
return false;
}
int diff = e - node.e;
if (diff == 0) {
return true;
}
if (diff < 0) {
return contains(node.left, e);
}
return contains(node.right, e);
}
//endregion
//region 删
public void remove(int e) {
root = remove(root, e);
}
private Node remove(Node node, int e) {
if (node == null) {
return null;
}
int diff = e - node.e;
if (diff < 0) {
node.left = remove(node.left, e);
return node;
}
if (diff > 0) {
node.right = remove(node.right, e);
return node;
}
//找到删除的结点进行删除
//只有右结点
if (node.left == null) {
Node right = node.right;
//node.right = null;
size--;
return right;
}
//只有左结点
if (node.right == null) {
Node left = node.left;
size--;
return left;
}
//左右结点都有
//找到比当前结点大的最小结点进行替换
//或者找到比当前结点小的最大结点进行替换
Node successor = min(node.right);
successor.right = removeMin(node.right);
successor.left = node.left;
node.left = node.right = null;
return successor;
}
private Node min(Node node) {
while (node.left != null) {
node = node.left;
}
return node;
}
private Node removeMin(Node node) {
if (node.left == null) {
Node rightNode = node.right;
node.right = null;
size--;
return rightNode;
}
node.left = removeMin(node.left);
return node;
}
//endregion
//region 高度
public int maxHeight() {
return maxHeight(root);
}
private int maxHeight(Node node) {
if (node == null) {
return 0;
}
return Math.max(maxHeight(node.left), maxHeight(node.right)) + 1;
}
public int minHeight() {
return minHeight(root);
}
private int minHeight(Node node) {
if (node == null) {
return 0;
}
return Math.min(maxHeight(node.left), maxHeight(node.right)) + 1;
}
//endregion
//region 前序遍历
public void preOrder() {
preOrder(root);
}
private void preOrder(Node node) {
if (node == null) {
return;
}
System.out.println(node.e);
preOrder(node.left);
preOrder(node.right);
}
public void preOrderNR() {
Stack<Node> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
Node cur = stack.pop();
System.out.println(cur.e);
if (cur.right != null) {
stack.push(cur.right);
}
if (cur.left != null) {
stack.push(cur.left);
}
}
}
//endregion
//region 中序遍历
public void midOrder() {
midOrder(root);
}
private void midOrder(Node node) {
if (node == null) {
return;
}
midOrder(node.left);
System.out.println(node.e);
midOrder(node.right);
}
//endregion
//region 后序遍历
public void postOrder() {
postOrder(root);
}
private void postOrder(Node node) {
if (node == null) {
return;
}
postOrder(node.left);
postOrder(node.right);
System.out.println(node.e);
}
//endregion
//region 层序遍历
public void levelOrder() {
Queue<Node> queue = new LinkedList<>();
queue.add(root);
while (!queue.isEmpty()) {
Node cur = queue.remove();
System.out.println(cur.e);
if (cur.left != null) {
queue.add(cur.left);
}
if (cur.right != null) {
queue.add(cur.right);
}
}
}
//endregion
public static void main(String[] args) {
//5
//2 7
// 6 8
BinarySearchTree tree = new BinarySearchTree();
tree.add(5);
tree.add(2);
tree.add(5);
tree.add(7);
tree.add(6);
tree.add(8);
tree.remove(7);
System.out.println(tree.contains(98));
//tree.preOrder();
//tree.preOrderNR();
//tree.midOrder();
//tree.postOrder();
System.out.println(tree.maxHeight());
System.out.println(tree.minHeight());
}
}
六、平衡二叉树
二分搜索树极端情况下会退化成链表,所以才有了avl 二分搜索树的基础上,对于任意一个结点,左子树和右子树的高度差不能超过1
平衡因子:左右子树高度差 高度:logn
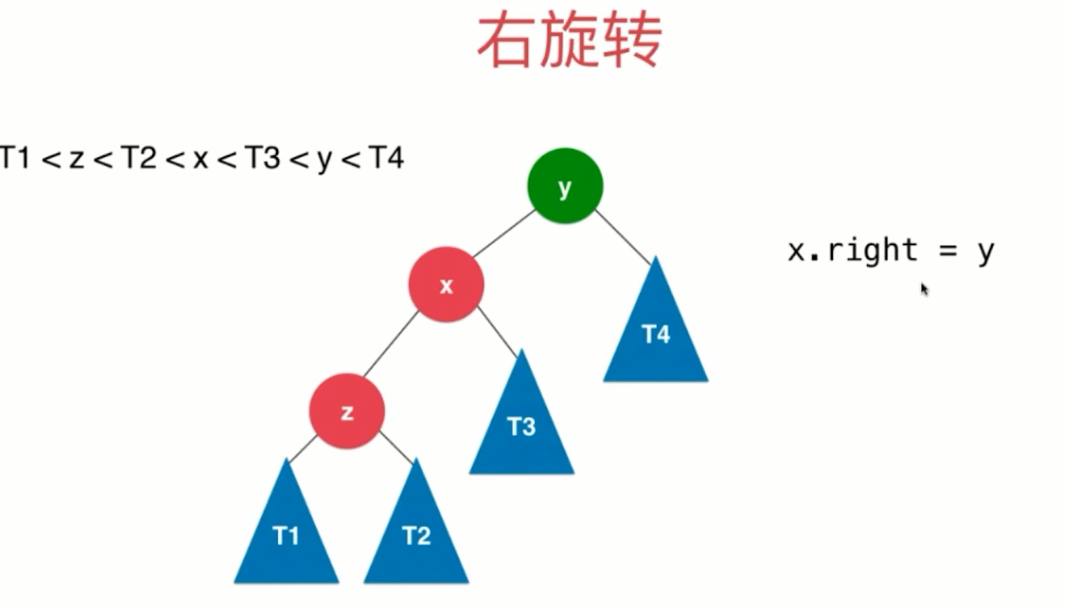
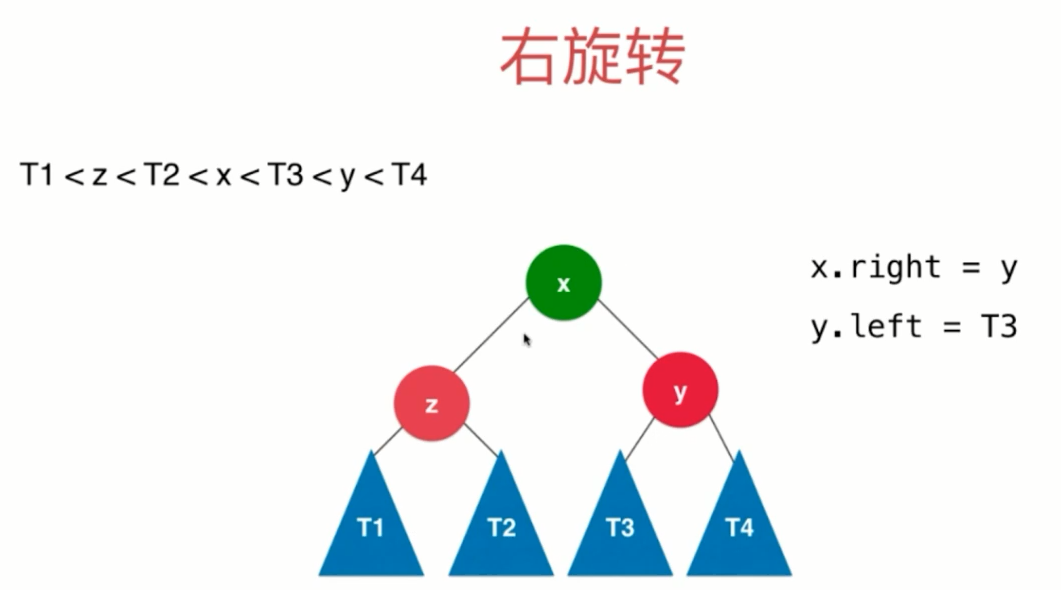
1)平衡操作
结点存储:高度、平衡因子 在插入(先插入到叶子结点)和删除时,如果结点不满足平衡性,则需要重新维护avl树的平衡性,一般有以下4种情况:
(1)LL
(2)RR
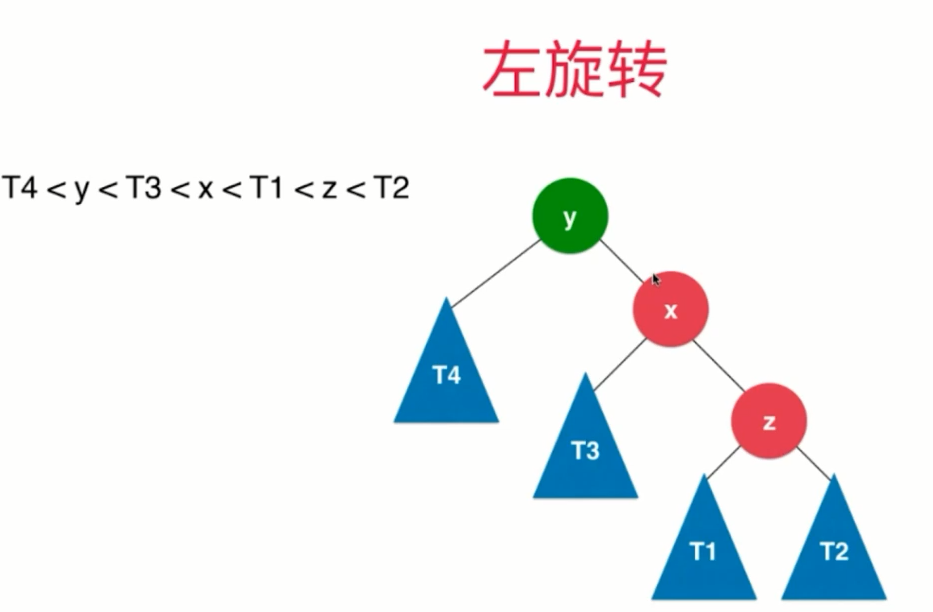
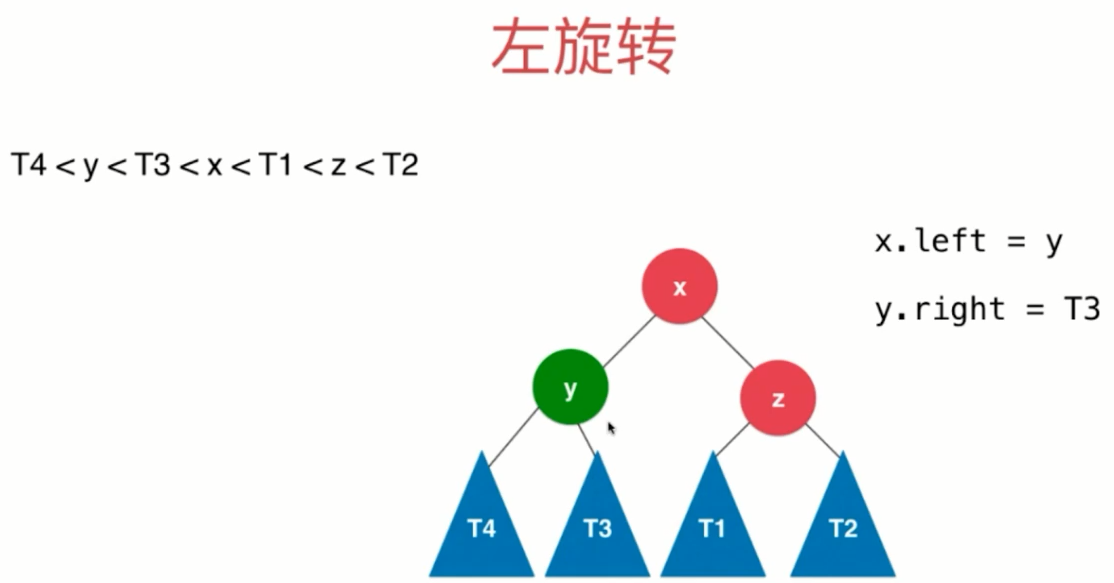
(3)LR
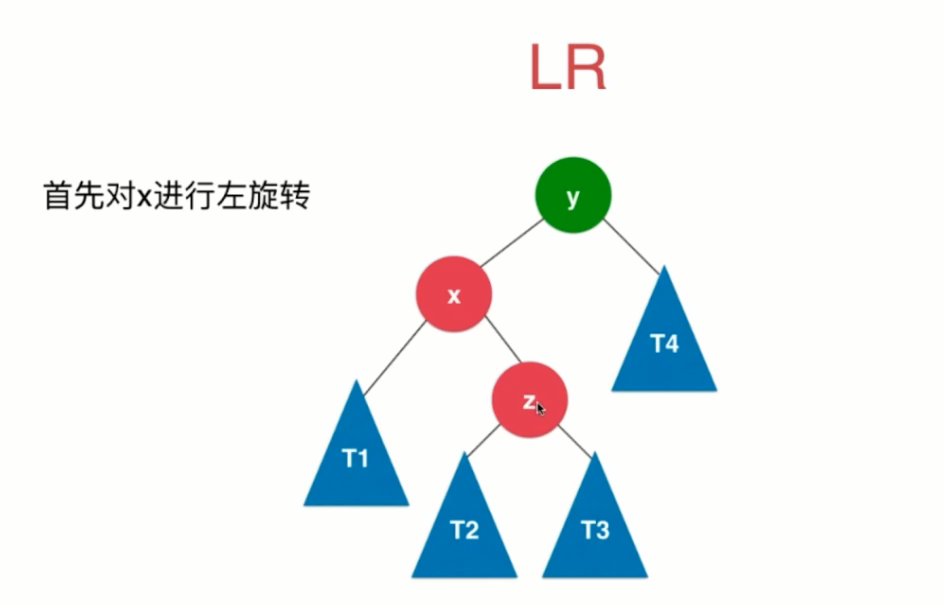
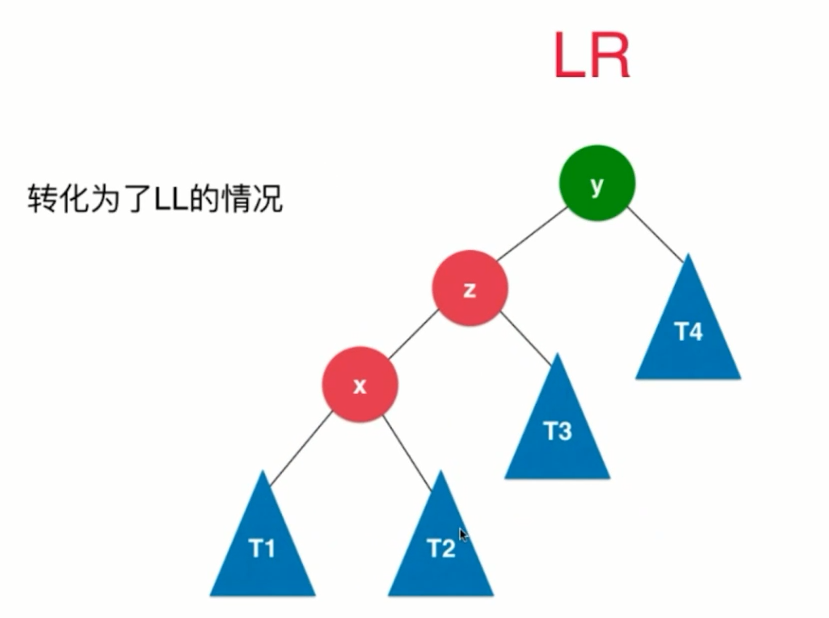
(4)RL
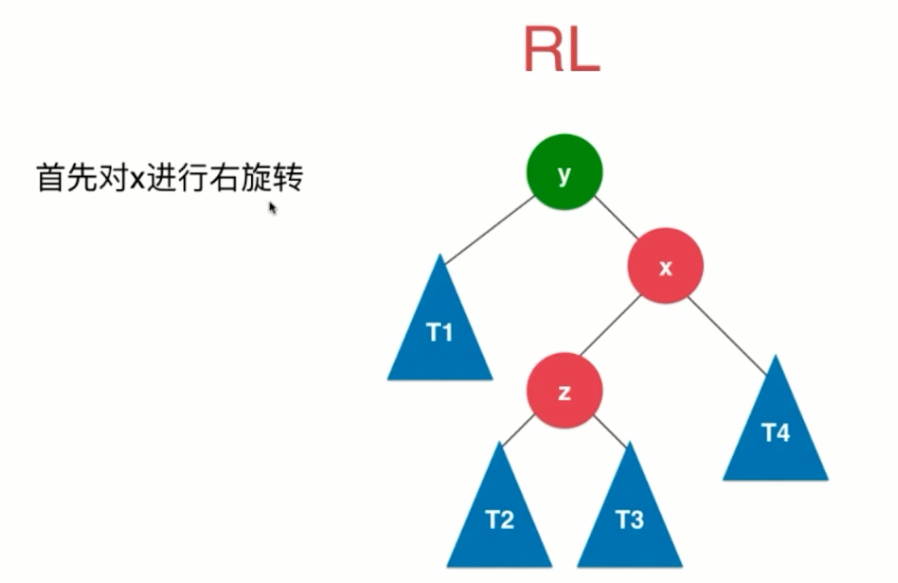
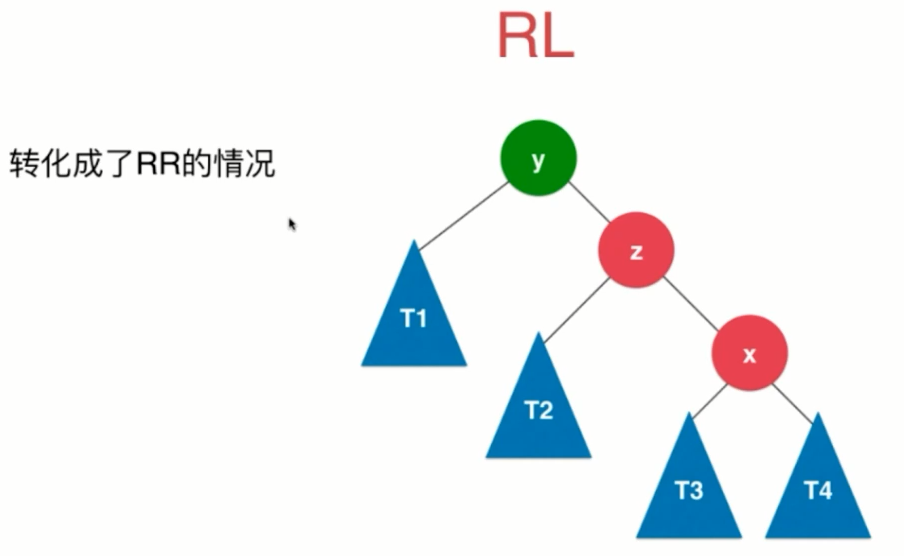
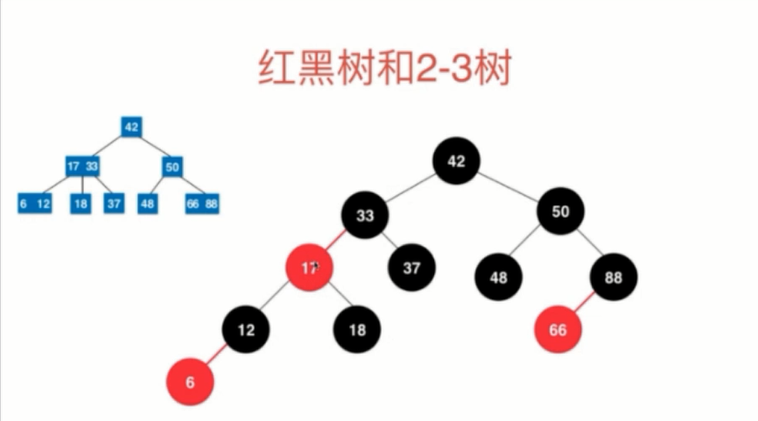
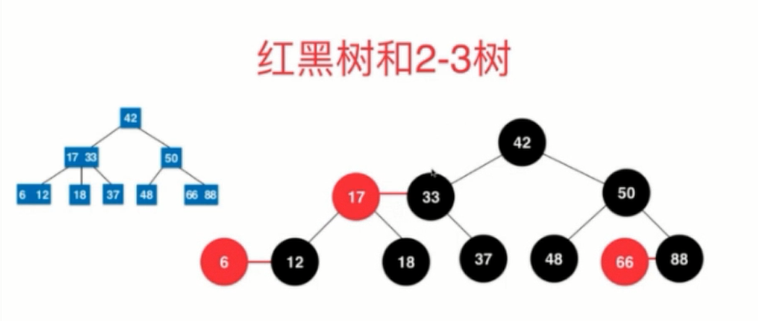
七、2-3树
平衡多路查找树,绝对平衡(每一层所有结点的高度一致),B树和B+树的基础都是此结构 也满足二分搜索树的基本特性 一个结点要么有2个孩子要么有3个孩子,即每个结点要么存1个数据或存2个数据
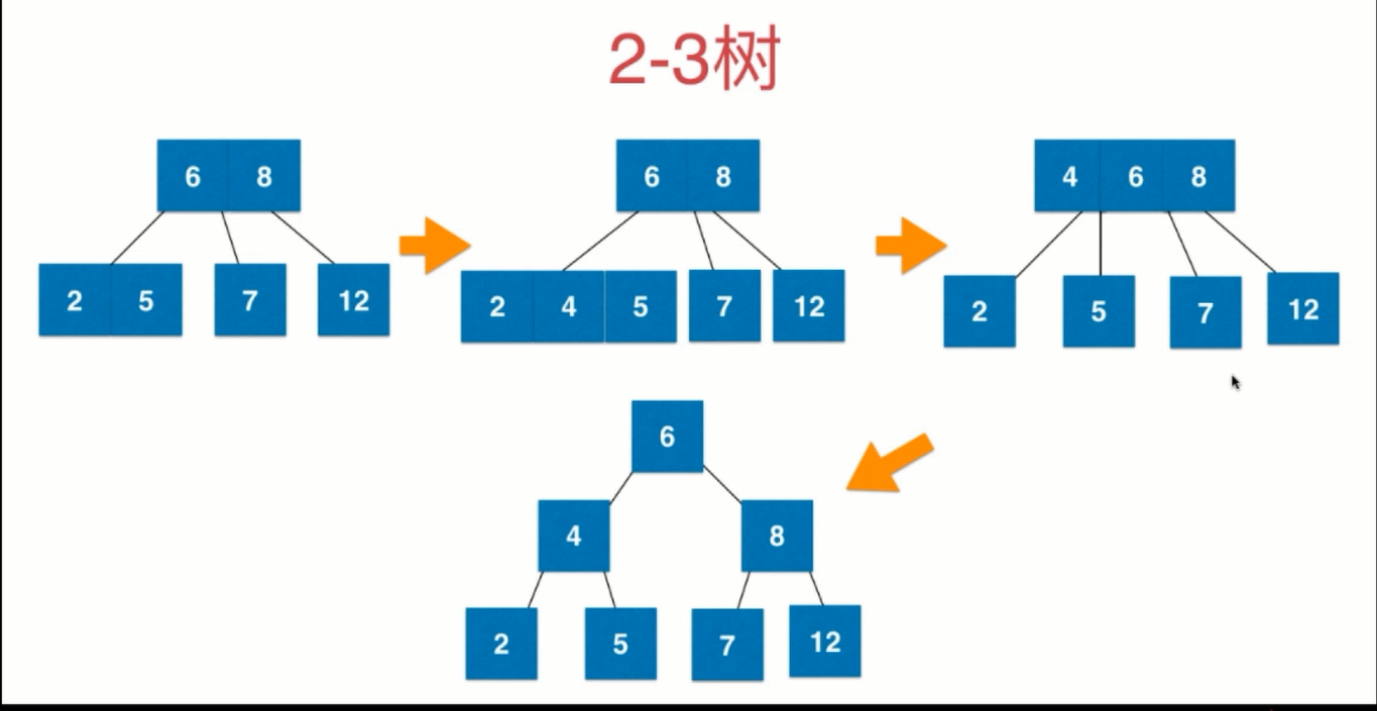
1)2-3树的新增
从根节点开始,向下插入到叶子结点 插入后的叶子结点是否超过3 否:结束 是:挑选插入后的叶子结点中的中间值向上融合 判断向上融合后的父结点是否超过3 以此类推
2)2-3树的删除
情况较多,比较复杂,最终在删除后需要通过左旋右旋保持最终的平衡
3)B树和B+树
2-3树就是一种B树
B+树和B树的区别: B+树在向上融合的时候,会在叶子结点保留一份向上融合的结点数据 也就是说,B+树的非叶子结点都会有一份相同的数据在叶子结点
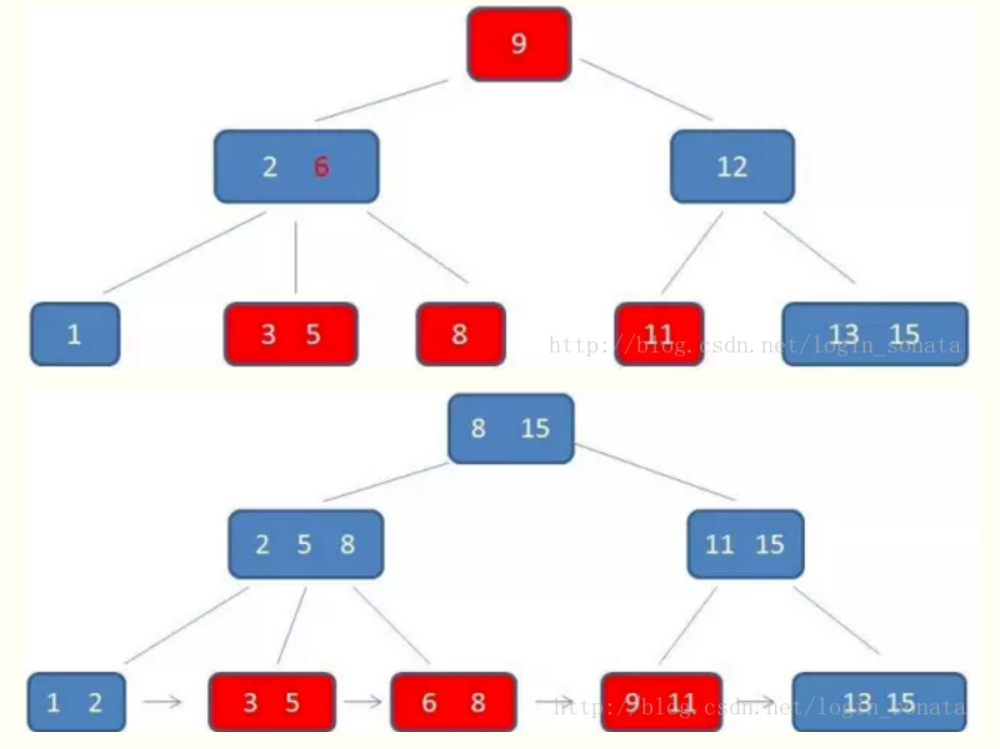
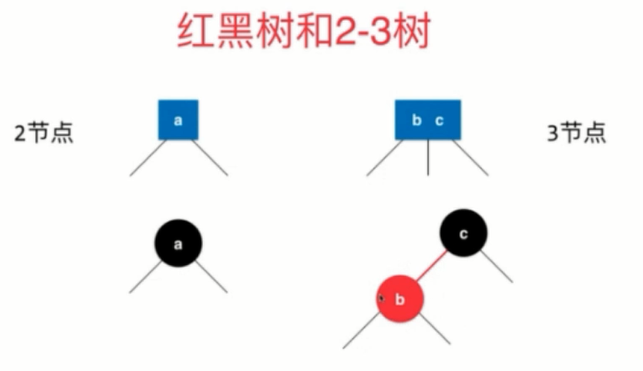
八、红黑树
红黑树和2-3的关系: 红黑树是用二叉树实现2-3树的一种结构,等价的,红结点代表2-3树中多值结点中的小值,其他结点都是黑结点
红黑树也是一种二分搜索树
1)性质
1)每个结点要么时黑色要么是红色 2)根结点是黑色 3)每一个叶子结点(指的真实叶子结点的孩子结点,即null)是黑色 4)如果一个结点是红色的,那么他的孩子是黑色的 5)黑平衡,不满足avl特性,从任意一个结点到叶子结点(null),经过的黑色结点是一样的
最大高度:2logn,O(logn)
九、常用树结构的比较
二分搜索树:对于完全随机的数据,普通二分搜索树新增/查询效果很好,但是如果是顺序的数据,就退化成了链表 avl树:对于查询较多的情况,avl树性能较好,新增/删除需要进行重平衡操作,耗性能 红黑树:牺牲了一点平衡性(2logn的高度),但是新增/删除性能较avl更优,